Im Folgenden wollen wir uns mit dem Einsetzungsverfahren beschäftigen. Dazu schauen wir uns am Anfang eine kurze Erklärung an und rechnen anschließend diverse Aufgaben durch.
Erklärung des Einsetzungsverfahrens:
Ziel des Einsetzungsverfahrens ist es aus einer der Gleichungen eines Gleichungssystems eine Variable zu entfernen, um so das Gleichungssystem zu lösen. Dieses Verfahren bietet sich vor allem an, wenn eine Gleichung bereits nach einer Variable aufgelöst ist. Wir legen direkt mit den Aufgaben los, da sich dieses Verfahren am besten durch die Anwendung erklären lässt.
1. Aufgabe mit Lösung

Wir sehen das die zweite Gleichung also 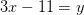


Wir sehen das diese Gleichung nur noch eine Variable enthält. Es gilt nun diese Gleichung zu lösen.

Den errechneten y-Wert können wir nun in eine der beiden Gleichungen einsetzen und den zugehörigen y-Wert errechnen. Wir wählen dazu die zweite Gleichung da diese bereits nach 

Demnach erhalten wir die Lösungsmenge
2. Aufgabe mit Lösung

Wir sehen das die zweite Gleichung 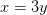
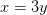

Nun können wir den errechneten y-Wert in eine der beiden Gleichungen einsetzen. Wir wählen die zweite Gleichung.

Demnach erhalten wir die Lösungsmenge
3. Aufgabe mit Lösung

Wir sehen das die zweite Gleichung bereits nach 

Den errechneten x-Wert können wir nun in die zweite Gleichung einsetzen.

Wir erhalten demnach die Lösungsmenge
4. Aufgabe mit Lösung

Wir sehen das die zweite Gleichung nach 

Nun können wir den errechneten y-Wert in die zweite Gleichung einsetzen.

Wir erhalten demnach die Lösungsmenge
5. Aufgabe mit Lösung

Nun haben wir den Fall in dem keine der beiden Gleichungen nach einer Variable aufgelöst ist. Da wir das Einsetzungsverfahren anwenden wollen, müssen wir als erstes eine der Gleichungen nach einer Variable auflösen. Wir entscheiden uns in dem Fall für die zweite Gleichung.

Wir lösen diese Gleichung nach 

Nun können wir diese Gleichung in die erste einsetzen.

Den errechneten x-Wert können wir nun in die zweite Gleichung einsetzen und den zugehörigen y-Wert berechnen.

Wir erhalten demnach die Lösungsmenge

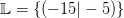

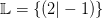
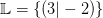

 (152 Bewertungen, Durchschnitt: 4,51 von 5)
(152 Bewertungen, Durchschnitt: 4,51 von 5)