Im Folgenden wollen wir uns mit der Multiplikation und Division beschäftigen. Es gibt zwei Regeln, die ihr wissen müsst:
Sind die Vorzeichen gleich, dann ist das Ergebnis positiv
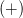
2. Regel:
Sind die Vorzeichen unterschiedlich, dann ist das Ergebnis negativ 
Mit diesen beiden Rechenregeln kann man schon einige Aufgaben bearbeiten. Legen wir direkt los.
1. Aufgabe mit Lösung

Wir sollten als Erstes realisieren, dass vor der Drei und Sieben sich noch ein Vorzeichen verbirgt. Deshalb schreiben wir es zuerst einmal zu:

Nun betrachten wir die Vorzeichen.
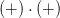
Wir erhalten demnach:

2. Aufgabe mit Lösung

Wir schauen uns im ersten Schritt die Vorzeichen an um zu entscheiden, ob das Ergebnis positiv oder negativ ist.
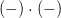
Es gilt also:

Nun haben wir das Vorzeichen bestimmt und können die Multiplikation durchführen.

3. Aufgabe mit Lösung

Im ersten Schritt betrachten wir die Vorzeichen um zu entscheiden, ob das Ergebnis positiv oder negativ lautet.

Es gilt demnach:

Nun können wir die Multiplikation durchführen.

4. Aufgabe mit Lösung

Kommen wir zur Division. Wir betrachten im ersten Schritt die Vorzeichen des Zählers und des Nenners.

Nach Regel 2 wissen wir, dass das Ergebnis negativ sein muss da im Zähler und Nenner unterschiedliche Vorzeichen sich befinden.
Nun können wir die Division durchführen.

5. Aufgabe mit Lösung

Wir betrachten die Vorzeichen des Zählers und des Nenners um zu entscheiden ob das Ergebnis positiv oder negativ ist.

ist nach der ersten Regel positiv.
Also erhalten wir:

6. Aufgabe mit Lösung

Als Erstes betrachten wir die Vorzeichen des Zählers und des Nenners und entscheiden ob das Ergebnis positiv oder negativ ist.

ist nach Regel 2 negativ.
Also gilt 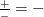

7. Aufgabe mit Lösung

Nun kommt ein etwas kompliziertes Beispiel. Wir betrachten nun die Vorzeichen des Zählers und des Nenners um zu entscheiden, ob das Ergebnis positiv oder negativ lautet. Dazu betrachten wir die Multiplikationen paarweise. Fangen wir also an und schreiben die Vorzeichen auf:

Wir betrachten nun das Vorzeichen 
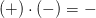

Nun betrachten wir den Zähler erneut und betrachten die Vorzeichen: 

Nun setzen wir ein und erhalten:

Das Ergebnis muss nun nach Regel 1 positiv sein. Wir können nun die Division durchführen und erhalten:

8. Aufgabe mit Lösung

Wir betrachten nun die Vorzeichen des Zählers und des Nenners.

Nun können wir die Vorzeichen wieder jeweils paarweise betrachten. Dazu setzen wir Klammern im Zähler.

Nach Regel 1 erhalten wir für den Zähler in der ersten großen Klammer positiv. Nach Regel 1 erhalten wir für den Nenner positiv.
Nun können wir vereinfachen und erhalten:

Nun betrachten wir den Zähler erneut. Nach Regel 2 erhalten wir für den Zähler ein negatives Vorzeichen.
Demnach erhalten wir:

Nun können wir dividieren bzw. kürzen und erhalten:

Die Multiplikation und Division und deren Berücksichtigung des Vorzeichens ist sehr wichtig, um Termumformungen generell zu verstehen und zu meistern.

 (7 Bewertungen, Durchschnitt: 4,43 von 5)
(7 Bewertungen, Durchschnitt: 4,43 von 5)