Im Folgenden wollen wir uns mit dem freien Fall im Vakuum beschäftigen. Der freie Fall stellt eine besondere Form der gleichmäßig beschleunigten Bewegung dar. Dabei wird in den Formeln, die wir aus der gleichmäßig beschleunigten Bewegung kennen, lediglich die Beschleunigung 
durch die Erdbeschleunigung 
ersetzt.
; der Weg 
wird für die Höhe 
ausgetauscht.
Des Weiteren lässt sich sagen, dass der Betrag der Fallbeschleunigung auf der Erdoberfläche nicht konstant ist. Er nimmt vom Äquator zu den Polen hin zu. Der Näherungswert für lautet 
. Die eigentliche Entstehung der Fallbeschleunigung lässt sich auf die Anziehungskraft der Erde zurückführen.
Beispiel 1:
Ein Stein fällt von einem hohen Gebäude.
a) Wie groß ist die Geschwindigkeit nach 
Sekunden?
Die Angaben sind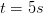 
und gesucht ist die Geschwindigkeit 
. Wir wählen die Formel 
aus und setzen ein.
Antwort: Der Stein hat nach Sekunden eine Geschwindigkeit von 
b) Welche Strecke hat der Stein nach Sekunden zurückgelegt.
Wir schreiben uns die Angaben heraus, 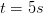. Um dieses Problem zu lösen, nutzen wir die Gleichung 
aus und setzen ein.
Antwort: Der Stein hat nach Sekunden eine Strecke von 
zurückgelegt.
c) Wie lange braucht der Stein, um eine Geschwindigkeit von 
zu erreichen?
Wir schreiben uns die Angaben heraus.
und 
ist gesucht.
Wir nutzen die Gleichung aus und stellen nach um.
Da keine Anfangsgeschwindigkeit gegeben ist, setzen wir 
.
Antwort: Der Stein braucht ungefähr 
, um eine Geschwindigkeit von zu erreichen.
Beispiel 2:
Carsten ist sehr mutig. Er lässt sich aus 
Höhe ins Wasser fallen.
a) Mit welcher Geschwindigkeit taucht er ins Wasser?
Wir schreiben uns zuerst die Angaben heraus.
und 
und gesucht ist .
Wir nutzen die Gleichung 
aus.
Da die Anfangsgeschwindigkeit beträgt, fällt diese Variable weg.
Nun müssen wir noch die Wurzel ziehen und erhalten:
Nun können wir unsere Werte einsetzen.
Antwort: Carsten taucht mit einer Geschwindigkeit von 
ins Wasser.
b) Wie lange braucht er, bis er ins Wasser eintaucht?
Wir haben die Höhe gegeben und die Zeit ist gesucht.
Die Geschwindigkeit und 
.
Wir nehmen die Gleichung 
und lösen die Gleichung nach auf.
und setzen ein.
Antwort: Carsten braucht bis er ins Wasser eintaucht.
Beispiel 3:
Von der Spitze eines Hochhauses (
) fällt ein Gegenstand auf die Straße. Wie lange braucht der Gegenstand für den Fall, und mit welcher Geschwindigkeit fällt er auf?
Wir schreiben uns die Angaben heraus.
Wir nutzen die Gleichung aus und stellen nach um.
Wir setzen ein,
Antwort: Der Gegenstand braucht 
.
Demnach sind nun die Angaben,
und . Gesucht ist noch .
Deshalb nutzen wir die Gleichung aus. Da die Anfangsgeschwindigkeit beträgt, fällt diese Variable weg.
Demnach haben wir die Gleichung 
.
Wir setzen die Werte ein
Antwort: Der Gegenstand fällt mit einer Geschwindigkeit von 
auf den Boden.
Beispiel 4:
Ein Falke erreicht bei dem herabstürzen, um seine Beute zu ergreifen, eine Geschwindigkeit von 
. Von welcher Höhe muss sich der Falke mindestens fallen lassen, um diese Geschwindigkeit zu erreichen?
Als Erstes schreiben wir uns die Angaben heraus.
Da nach der Höhe gefragt ist, nutzen wir die Gleichung aus und stellen nach um.
Da beträgt, fällt diese Variable weg.
Nun setzen wir ein:
Antwort: Die Höhe, aus der sich der Falke mindestens fallen lassen muss, beträgt 
.
Beispiel 5:
Ein Brunnen ist 
tief. Nach welcher Zeit hört man den Aufprall eines los gelassenen Steins? (Die Schallgeschwindigkeit beträgt 
)
Die Angaben sind 
und gesucht ist die Zeit .
Als Erstes berechnen wir wie lange der Stein braucht, bis er auf den Brunnen Boden aufprallt. Wir benutzen dazu die Formel 
und stellen nach 
um.
Wir setzen die Werte ein und erhalten
Der Stein prallt also nach 
auf.
Nach dem Aufprall kommt der Schall ins Spiel. Da der Schall eine konstante Geschwindigkeit besitzt, können wir hier die Formel für die gleichförmige Bewegung anwenden und zwar 
. Wir tauschen die Variable 
für Weg durch die Höhe aus und lösen diese Gleichung nach auf und erhalten 
.
Wir setzen die Werte ein, die uns für die Schallgeschwindigkeit angegeben wurden.
Die Gesamtzeit beträgt nun 
Antwort: Man hört den Aufprall nach 
.
(19 Bewertungen, Durchschnitt: 3,32 von 5)
Loading...
